Finding a relation between Mean Median and Mode difficult in your statistics? Let’s read about all of them one by one in a detailed form.
Before getting into an empirical relation between Mean Median and Mode, let us first see what they individually mean.
What is Mean?
Mean is just another word for average.
What is the Median?
Median is nothing but the mid number in your set of numbers.
What is Mode?
The mode is the most frequent number used in your set of numbers.
The relation between Mean Median and Mode:
The relation between Mean Median and Mode is:
The distinction between Mean and Mode is 3 times of distinction between Mode and Median.
Mean – Mode = 3 (Mean – Median)
Mean Vs Median
- Mean is nothing but an average which is found by adding all the numbers and dividing it by the number of items in the set.
For example,
The set of numbers taken will be 10, 12, 14, 20, 30
Mean = Sum of the numbers/number of items in the set.
= 10+12+14+20+30/5
= 86/5
= 17.2
So, here Mode is 17.2
- The Median is putting the numbers in an ascending number and finding an exact middle number.
So, as per the above set of numbers, the median will be 14.
But if a situation comes, where you have the data set of even numbers like
For Example: 6,12,4,16,12,20 that’s 6
For finding a Median here will be
firstly, arranging them in ascending order to descending order
4,6,12,12,16,20
Here, Median = Sum of the most frequent used Numbers / 2
= 12+12/2
= 24/2
= 12
So, the Median is 12 here.
Mean Vs Average
In the relation between Mean Median and Mode, do not get confused between Mean and Average, they are just two words with same meanings. Yes, the average is also taken out by adding the numbers and diving it by the number of items you have
Like, 10+6+20/3 will be the average of 10,6 and 20 which is 12.
The Mean is also the same.
Mean is a short term for Arithmetic Mean. You will find different words in statistics because there are different types of means and they all have different meanings. We will read about that in detail.
Let’s take an example:
In a moderately skewed distribution, the value of the median is 30 and the value of the Mean is 32.5. what will be the value of Mode?
Median = 30
Mean = 32.5
Let us take the value of Mode as X
Let’s recall the formula
Mean – Mode = 3 (Mean – Median)
32.5 – x = 3 (32.5 – 30)
32.5 – x = 3 * 2.5
32.5 – x = 7.5
32.5 – 7.5 = x
26.0 = x
Therefore, Mode is 26.
Also read: Top 10 Differences Between Grid Computing and Cloud Computing
There are different types of means. Let us look at all of those types one by one:
-
Harmonic Mean:
In the relation between mean median and mode, Harmonic Mean works with reciprocating the numbers like the numerator go into the denominator and vice-versa.
For example, the Harmonic Mean of 2,6 and 6 can be solved as:
3 divided by 1/2+ 1/6 + 1/8
= 3/1.2
= 2.5
So, the Harmonic Mean is 2.5.
The means help to hunt out increasing or divisor relationships between fractions without fear regarding common denominators. Harmonic implies that unit is sometimes utilized in averaging things like rates (e.g., the common travel speed given an amount of the many trips). The weighted mean is used in finance to average multiples similar to the price-earnings relation as a result of it offers equal weight to each info using a weighted mean to average these ratios would provide larger weight to high information points than low information points as a result of price-earnings ratios don’t seem to normalized price even though the earnings are equalized.
This is used in physics. It is much better than Arithmetic Mean in the case of ratio and rates. The use of this also happens in geometry, finance, and computer science. For example
-
Arithmetic- Geometric Mean
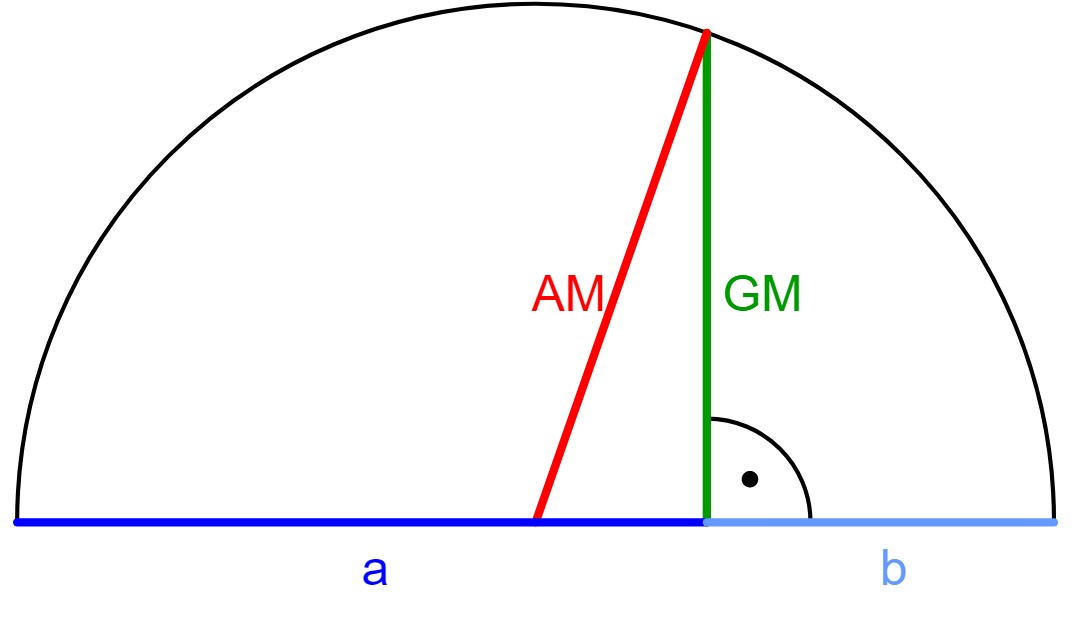
Arithmetic – Geometric Mean.
It is mainly used for computer calculations. It was first developed by Gauss to calculate planetary orbits. As the name says, it is a mixture of Arithmetic and Geometry. Quite a complicated one, but you can find the details by clicking here.
-
Weighted Mean:
This type is very common while reading about statistics. Other than the contribution of a data set towards finding an average, some data points contribute more than others. If all the weights are equal then this will equal the arithmetic mean.
-
Root Mean Square
Also called Quadratic Average, this is usually used in sine waves, like Electrical Engineering.
For calculating Sine Waves the formula is
This square is used to measure the magnitude of a set of numbers by
- Squaring each number
- Find the mean of these squares
- Finding the square root of the average
-
Heronian Mean
It is used in Geometry to find out the value of a pyramid with the tip cut off. Such pyramids are called a Pyramidal Frustum.
-
Geometric Mean
This has a specific use in social science, technology, and finance. For example, if your stock earns 20% in the first year, 30% in the second year, and 40% in I third year. How will you know the average rate of returns? Remember, you cant use Arithmetic Mean here as you are not adding you need to multiply the rates of return.
Let us now read about the difference between Harmonic Mean, Arithmetic Mean, and Geometric Mean:
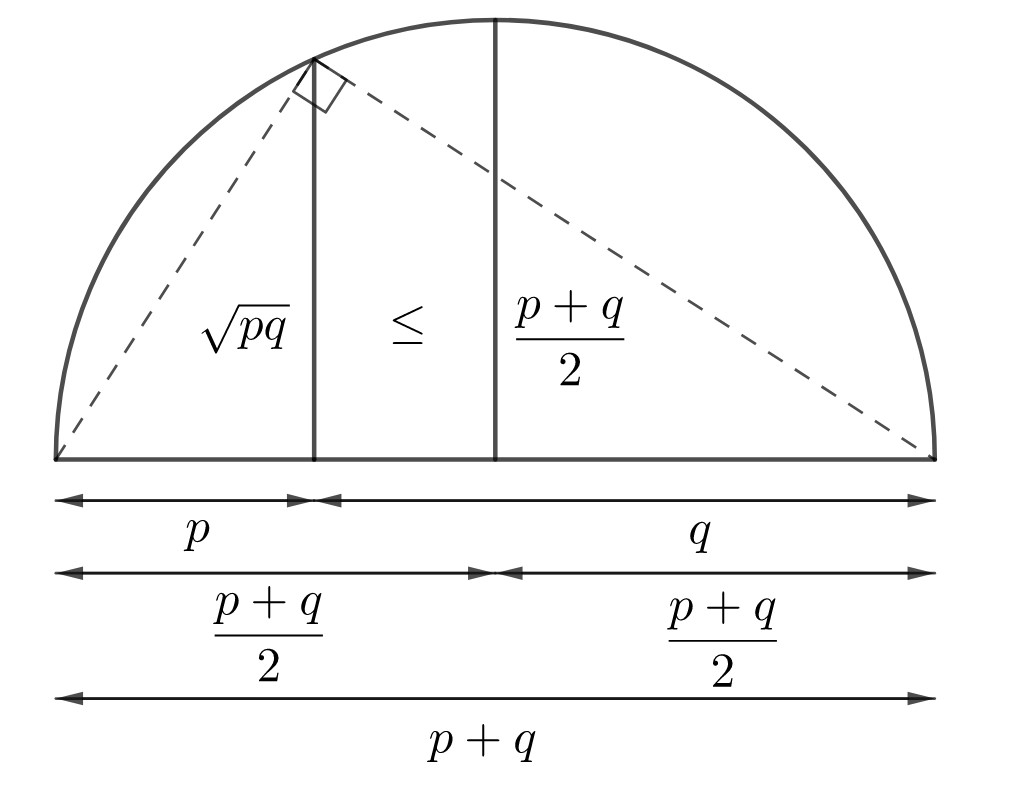
The arithmetic mean can be found out by just adding the adding all the numbers and dividing it by the number of items there in the set. If you have to find the average of class test scores you would simply add the test scores and divide it by the number of students.
For example, 4 students gave the exam and their scores are 40%, 50%, 60%, and 70%. The average would be
40+50+60+70/4
= 220/4
= 55
The arithmetic mean is 55%
The Geometric Mean is used to calculate the performance result of an investment. it is pronounced as “the nth root product of n numbers”
Geometric Means are usually used while dealing with percentages that are derived from its values and Arithmetic Mean deals with their values.
The Harmonic Mean is used for rates or multiples.
The relation between Mean, Median, and Mode in terms of frequency distribution:
-
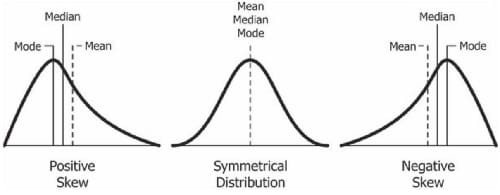
Frequency Distribution with Symmetrical Curve:
In this place, the relation between Mean Median and Mode is that they are all equal to each other.
That is: Mean=Mode=Median
-
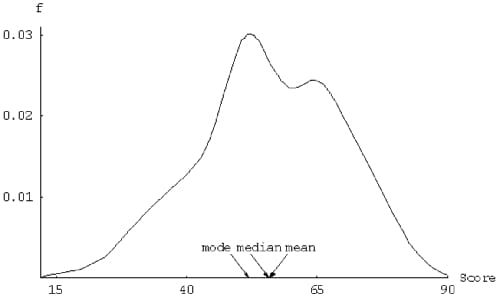
Positively Skewed Frequency Distribution
In this place, the relation between Mean Median and Mode is that the mean is always greater than the median and the median is greater than the mode.
That is: Mean > Median > Mode
-
Negatively Skewed Frequency Distribution
In this place, its exactly opposite to the positive one. Here, the relation between Mean Median and Mode will be that the Mean is always lesser than Median and Median is always lesser than Mode.
That is: Mean < Median < Mode
Let us look at the relation between Mean Median Mode as per technology
SPSS Mean Mode Median:
Let us see the relation between Mean Median and Mode in terms of technology
The use of the frequency tab is required for finding the SPSS mean median and mode. SPSS is very much similar to Excel. If you know how to use MS Excel, you can easily learn this. It may look like counter-intuitive, but the descriptive statistics tab doesn’t help you in taking out the value of Mode or Median.
Refer to this video to understand the steps for its usage in technology.
The relation between Mean Median Mode as per TI 83
The value of TI 83 Mean or TI 83 Median can be found in two ways:
Either by entering a list of numbers or data or by the utilization of the home screen to type commands. The former way is as easy as the latter one. You have the advantage of using the data for different purposes once you are done with you Mean, Median, and Mode calculation.
Refer to this video to understand the steps for your detailed understanding.
