Velocity gradient such a difficult and unknown word for the one who is the beginners in science and wanted to learn about something useful.
This article will help you to understand velocity and velocity gradient.The Velocity gradient is the most essential one to identify and analyse the path involving path-dependent materials.
Velocity:
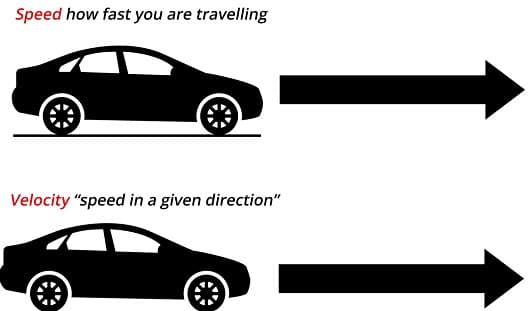
In simple words, Velocity can be defined as,” The direction or the movement of the body or the object”. The velocity is equivalent to a specification of an objects speed or direction of motion.
It is the prime indicator of the position as well as the speed of the object. It can also be defined as ” Distance covered by the object in unit time”. It is a physical vector quantity with magnitude and direction.
The velocity of an object is the rate of its position concerning a frame of reference, and the function of time.
The dimensional formula of the velocity is defined as the expression of the physical quantity in terms of its basic unit with proper dimensions. It can also be defined as speed in a specific direction.
Mathematically, Velocity = Displacement / Time. Dimensional Formula of Displacement = M0L1T0. There are many types of velocity like constant velocity, uniform velocity, Non-uniform velocity, average velocity and instantaneous velocity etc.
Constant Velocity:
The motion with constant velocity is the simplest form of motion. The constant motion when an object slides over a horizontal, low friction service.

Uniform Velocity:
If the magnitude and direction of the velocity remain constant without any change, then it is known as Uniform Velocity.
Non-Uniform Velocity:
If the magnitude and direction of the velocity without remaining constant, if it changes then it is known as Non-Uniform velocity.
Average Velocity:
The ratio of the total displacement and the total time taken by the particular particle is known as Average velocity.
Instantaneous Velocity:
The velocity of a particle at a particular instant or movements is known as Instantaneous velocity.
For example: When the change of direction occurs while the cars racing on the curved tracks, their velocity will be constant. This is known as Velocity.
Gradient:
The gradient or gradient vector field of a scalar function f(x1, x2, x3, …, xn) is denoted ∇for ∇→f where ∇ denotes the vector differential operator, del. The notation grad f is also commonly used to represent the gradient.
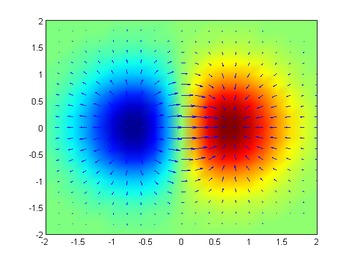
The gradient of f is defined as the unique vector field whose dot product with any vector v at each point x is the directional derivative of f along with v.
The gradient is a vector operation which operates on a scalar function to produce a vector whose magnitude is the maximum rate of change to the function point is gradient. The divergence of the gradient is called LaPlacian.
The rate at which the mountain gets steeper is the example of the Gradient.
The gradient can be explained in many subjects like mathematics, physics, fluid mechanics etc. In mathematics, it is a differential operator that is applied to a three-dimensional vector-valued function.
In physics, it is the rate of change concerning the distance of variable quantity and also the curve representing such a rate of change.
In Science, you can identify from the word “Grade” that mentions and also describes the incline, slope or degree in temperature, pressure or even colour. This is known as the Gradient.
Velocity Gradient:
In simple words, Velocity gradient can be defined as,” The difference in Velocity between adjacent layers of the fluid is known as Velocity gradient”.
from lboro.ac.uk)
It is also defined as the gradient of the spatial description of the velocity and is called the rate of deformation tensor and vorticity sensor, respectively. And it is also given by v/x where v is the velocity difference and x is the distance between layers.
To keep one layer of fluid moving at a greater velocity than the adjacent layer, a force F is necessary, resulting in a shearing stress F/A, where A is the area of the surface in contact with the layer being moved
The SI Unit of the Velocity gradient is 1/sec= per second. In fluid mechanics and also the continuum mechanics, the velocity gradient describes the velocity of the fluid that changes between different points. The SI Unit is Kelvin per meter (k/m).
Velocity can also be defined as the rate of change in velocity per unit of distance and mathematically it can be derived as Velocity Gradient = Velocity/ Distance. In fluid mechanics, it is defined as the variation in the velocity among the adjacent layers of the fluid.
The difference in the flow of the velocity between the adjacent layers of the fluid is measured in the Velocity gradient. The temperature gradient is a dimensional quantity expressed in the unit of degrees per unit length.
All gradients like Velocity gradient, potential gradient and magnetic field gradient has both magnitude and direction but it is scalar as it doesn’t follow the vector algebra.
The rate of momentum transfer per unit area, between two adjacent layers of fluid, is proportional to the negative value of the velocity gradient between them. This ratio is called the kinematic viscosity of a fluid, v, and has the dimensions of L2 t-1.
The dimensional formula of velocity gradient is given by,
[M0 L0 T-1]
Where,
- M = Mass
- L = Length
- T = Time.
The amount of friction depends on the fluid viscosity and the velocity gradient (that is, the relative velocity between fluid layers). The velocity gradients are set up by the no-slip condition at the wall. … When a fluid is stationary, its molecules are in a constant state of motion with a random velocity.
For example, the rate of change of displacement is called velocity. So in your case velocity gradient means how is the magnitude of velocity varies with distance.
For example: when fluid is flowing through a pipe velocity of each layer is defined from the axis of the cylindrical pipe. This is known as the Velocity Gradient.
This article will help you know about the Velocity gradient for those who are the beginners in learning about the Velocity gradient. It will also help you know about the Velocity and its types.